Ejemplo de álgebra en programación: Intersección de dos Intervalos

¡Saludos visitante! si deseas comentar o hacer una pregunta sobre este post por favor dirígete a la nueva dirección en http://variabletecnica.com.ve. La página que estás leyendo dejará de estar disponible el 15/11/2015. Gracias, y disculpa las molestias 🙂

Usualmente al hacer una consulta SQL para devolver los registros sobre un rango de fechas (o cadenas, o números…) haríamos uso de desigualdades (o usamos la cláusula BETWEEN):

SELECT  campo1, campo2
FROM    mi_tabla
WHERE   (otras_condiciones_aquí)
    AND fecha &gt;= inicio_rango
    AND fecha &lt;= fin_rango

Donde fecha es el campo de la tabla mi_tabla que queremos probar dentro del rango especificado desde inicio_rango hasta fin_rango, incluyendo los valores extremos.

El siguiente gráfico muestra los cinco casos posibles para los registros de la tabla. Entre ellos vemos que los casos 2, 3 y 4 son los que queremos que entren a los resultados de la consulta, mientras que los casos 1 y 5 quedarán por fuera.

Simple, ¿verdad?

Subiendo el nivel

Hace poco tuve que hacer una consulta SQL donde debía hallar aquellos registros cuyos rangos (inicio y fin) interceptaran cierto rango especificado.

Mientras escribía la consulta, que ya era bastante complicada aun sin los rangos de fechas, hice una lista mental de los posibles casos de intervalos. Cuando llegué al sexto caso me levanté y lo escribí en la pizarra (no es fácil escribir una cosa mientras piensas en otra…).

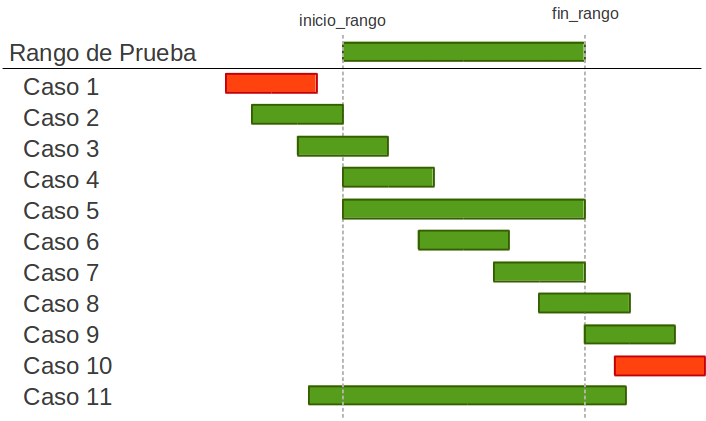
Ya no es tan simple, ¿verdad? Obviamente tenía que agrupar los casos posibles o tendría que agregar varios OR al SELECT, y no creo que eso sea bueno para el rendimiento, veamos:

Los casos 2 y 3 son equivalentes: en el caso 2 la fecha final del registro coincide con el inicio del rango, así que se considera que hay intersección y entra en el resultado (por lo menos para mi consulta se debe considerar dentro).
Los casos del 4 al 7 son equivalentes: todos ellos están completamente dentro del rango.
Los casos 8 y 9 son equivalentes: en el caso 9 la fecha inicial del registro coincide con el fin del rango, así que se considera que hay intersección.
El caso 11: este es especial y problemático, porque ni el inicio ni el fin entran en el rango, pero aun así debe entrar en el resultado.
Los casos 1 y 10: estos dos no son equivalentes entre sí, pero como no son los que quiero simplemente no les prestaré atención por ahora (aunque de haberlos considerado me habría ahorrado como media hora…).

Así que me puse manos a la obra y empecé con mi consulta, que ahora tendría las pruebas de los cuatro casos, separadas por OR:

SELECT  campo1, campo2
FROM    mi_tabla
WHERE   (otras_condiciones_aquí)
    AND (
        (inicio &lt; inicio_rango AND fin &gt;= inicio_rango) OR
        (inicio &gt;= inicio_rango AND fin &lt;= fin_rango) OR
        (inicio &lt;= fin_rango AND fin &gt; fin_rango) OR
        (inicio &lt; inicio_rango AND fin &gt; fin_rango)
    )

Pero mientras escribía lo anterior pensé ¿No sería más corto decir NOT (caso_1 OR caso_10) en lugar todo esto?

Logro desbloqueado: maestro en álgebra booleana

Veamos como sería. El Caso 1 podemos escribirlo como fin < inicio_rango, y el Caso 10 como inicio > fin_rango. Entonces tendríamos:

NOT ( (fin &lt; inicio_rango) OR (inicio &gt; fin_rango) )

Bien, ahora un poco de álgebra booleana para simplificar (usualmente evitaremos usar OR en consultas SQL). Usando una de las Leyes de De Morgan:

NOT (A OR B) = NOT A AND NOT B

Nuestra condición queda como:

(fin &gt;= inicio_rango) AND (inicio &lt;= fin_rango)

Y nuestro SELECT:

SELECT  campo1, campo2
FROM    mi_tabla
WHERE   (otras_condiciones_aquí)
    AND fin &gt;= inicio_rango
    AND inicio &lt;= fin_rango

Que es muy parecido al caso de una sola fecha en un rango.

Mi primer intento con todas las condiciones también funcionaba, pero ésta solución es más elegante y fácil de entender, además de que puede ser más eficiente para su ejecución si las tablas son grandes.

Este pequeño ejercicio está basado en SQL, pero la lógica aplica igual para una condición en cualquier lenguaje de programación. Algo interesante que noté en esta situación es que hay que pensar un par de minutos antes de resolver un problema, incluso si ya sabes la solución, porque tal vez la solución que escogiste al primer intento no sea la más simple.

Ahora mismo se me ocurre un par de ejemplos de como pensar linealmente te lleva a soluciones ineficientes e incluso ineficaces, pero eso será para el próximo artículo.

Referencias

Álgebra Booleana (axiomas y teoremas): http://es.wikipedia.org/wiki/%C3%81lgebra_de_Boole#L.C3.B3gica_binaria

Cita del día

La lógica te llevara desde A hacia B, la imaginación te llevará a todas partes.
Albert Einstein